46 排序的基本概念
排序的基本概念(一)
-
排序的一般定义
- 排序是计算机内经常进行的一种操作,其目的是将一组“无序”的数据元素调整为“有序”的数据元素。
例如:将下列关键字序列 52,49,80,36,14,58,61,23,97,75 调整为: 14,23,36,49,52,58,61,75,80,97
-
排序的数学定义 假设含n个数据元素的序列为:
{R<sub>1</sub>,R<sub>2</sub>,...,R<sub>n</sub>},其相应的关键字序列为:{K<sub>1</sub>,K<sub>2</sub>,...,K<sub>n</sub>}; 这些关键字相互之间可以进行比较,即:在它们之间存在着这样一个关系: Kp1≤Kp2≤...≤Kpn 按此固定关系将上式记录序列重新排列为:{R<sub>p1</sub>,R<sub>p2</sub>,...,R<sub>p3</sub>}的操作称为排序。 -
排序的示例
初始按编号排序
编号 姓名 内功 外功 情商 智商 总评 1 郭靖 92 91 85 70 338 2 张无忌 84 89 80 85 338 3 令狐冲 89 93 89 90 361 4 杨过 92 93 90 90 365 按总评排序
编号 姓名 内功 外功 情商 智商 总评 4 杨过 92 93 90 90 365 3 令狐冲 89 93 89 90 361 2 张无忌 84 89 80 85 338 1 郭靖 92 91 85 70 338 -
问题 按总评排序后为什么张无忌的排名比郭靖靠前呢?
-
排序的稳定性 如果在序列中有两个数据元素r[i]和r[j],他们的关键字k[i]==k[j],且在排序之前,对象r[i]排在r[j]前面;如果在排序之后,对象r[i]仍在对象r[j]的前面,则称这个排序方法是稳定的,否则称这个排序方法是不稳定的。
-
稳定性排序示例
初始按编号排序
编号 姓名 内功 外功 情商 智商 总评 1 郭靖 92 91 85 70 338 2 张无忌 84 89 80 85 338 3 令狐冲 89 93 89 90 361 4 杨过 92 93 90 90 365 按总评排序
编号 姓名 内功 外功 情商 智商 总评 4 杨过 92 93 90 90 365 3 令狐冲 89 93 89 90 361 1 郭靖 92 91 85 70 338 2 张无忌 84 89 80 85 338 -
多关键字排序
- 排序时需要比较的关键字多余一个
- 排序结果首先按关键字1进行排序
- 当关键字1相同时按关键字2进行排序
- ......
- 当关键字n-1相同时按关键字n进行排序
-
多关键字排序示例
初始按编号排序
编号 姓名 内功 外功 情商 智商 总评 1 郭靖 92 91 85 70 338 2 张无忌 84 89 80 85 338 3 令狐冲 89 93 89 90 361 4 杨过 92 93 90 90 365 按(内功,外功)排序
编号 姓名 内功 外功 情商 智商 总评 4 杨过 92 93 90 90 365 1 郭靖 92 91 85 70 338 3 令狐冲 89 93 89 90 361 2 张无忌 84 89 80 85 338 -
问题 多关键字排序是否比单关键字排序更复杂? 对于多关键字排序,只需要在比较操作时同时考虑多个关键字即可!
编程实验
-
多关键字比较操作
#include <QCoreApplication>
#include <QDebug>
class Data
{
public:
Data(int i,int j):num1(i),num2(j){}
bool operator <(const Data &obj){
return (num1<obj.num1)||((num1==obj.num1)&&(num2<obj.num2));
}
bool operator >(const Data &obj){
return (num1>obj.num1)||((num1==obj.num1)&&(num2>obj.num2));
}
bool operator >=(const Data &obj){
return !(*this<obj);
}
bool operator <=(const Data &obj){
return !(*this>obj);
}
private:
int num1; //high
int num2; //level
};
int main(int argc, char *argv[])
{
QCoreApplication a(argc, argv);
Data data1(3,5);
Data data2(2,6);
Data data3(3,4);
qDebug()<<(data2<data1);
qDebug()<<(data3<data1);
return a.exec();
}
排序的基本概念(二)
-
排序中的关键操作
- 比较
- 任意两个数据元素通过比较操作确定先后次序
- 交换
- 数据元素之间需要交换才能得到预期结果
- 比较
-
排序的审判
- 时间性能
- 关键性能差异体现在比较和交换的数量
- 辅助存储空间
- 为完成排序操作需要额外的存储空间
- 必要时可以“空间换时间”
- 算法的实现复杂性
- 过于复杂的排序法可能影响可读性和可维护性
- 时间性能
-
KylinLib中的排序类类设计
class Sort : public Object {
private:
Sort();
Sort(const Sort&);
Sort& operator=(const Sort&);
template<typename T>
static void swap(T &a,T &b){
T c(a);
a = b;
b = c;
}
public:
//...
}
编程实验
-
KylinLib中的排序类
小结
- 排序是数据元素从无序到有序的过程
- 排序具有稳定性,是选择排序算法的因素之一
- 比较和交换是排序的基本操作
- 多关键字排序与单关键字无本质区别
- 排序的时间性能是区分排序算法好坏的主要因素
47 选择排序和插入排序
选择排序
-
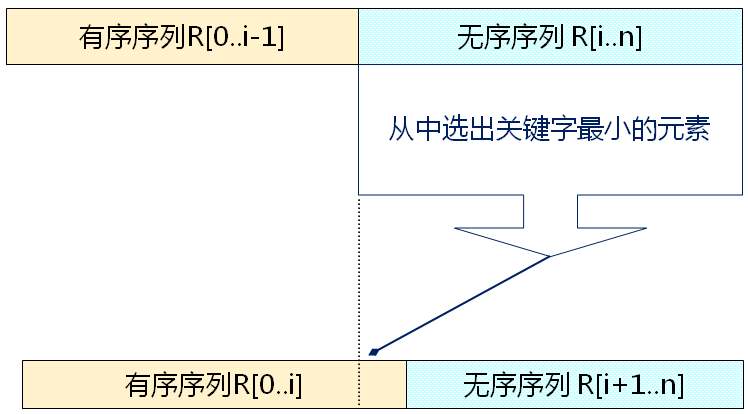
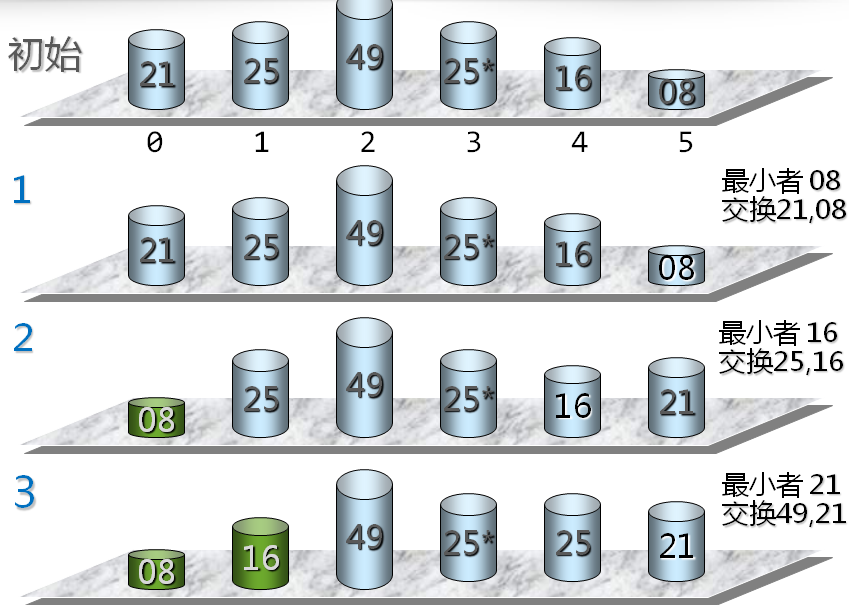
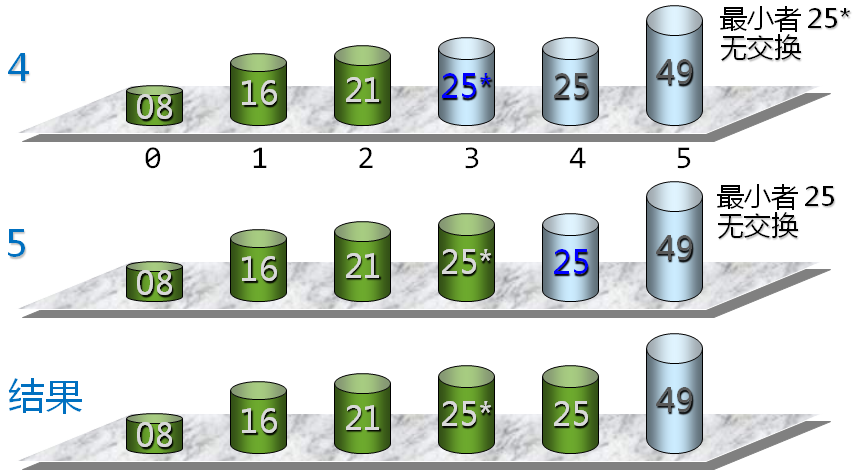
选择排序的基本思想 每次(例如第i次,i=0,1,...,n-2)从后面n-i个待排的数据元素中选取关键字最小的元素,作为有序元素序列第i个元素。
-
第i次选择排序示例
编程实验(一)
-
选择排序的实现
template<typename T>
static void select(T array[],size_t size){
for (size_t i=0;i<size;i++) {
size_t index = i;
for (size_t j=i+1;j<size;j++) {
if(array[j]<array[index])
index = j;
}
if(index!=i) swap(array[i],array[index]);
}
}
插入排序
-
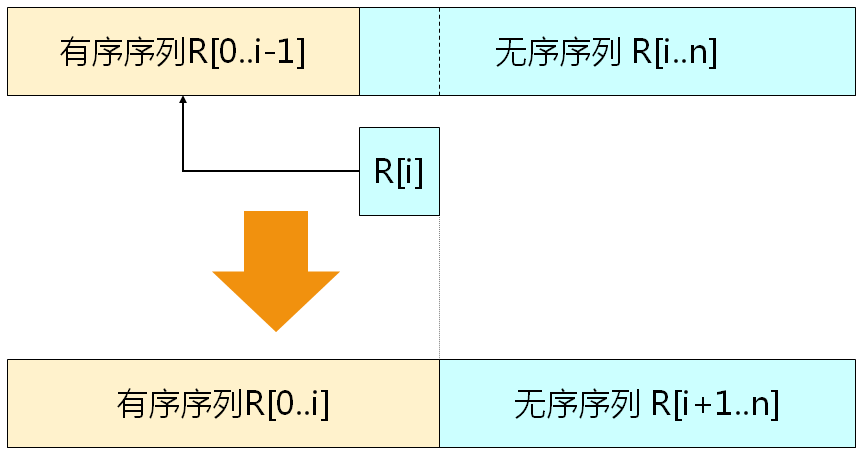
插入排序的基本思想 当插入第i(i>=1)个数据元素时,前面的V[0],V[1],...,V[i-1]已经排好序;这时,用V[i]的关键字与V[i-1],V[i-2],...,V[0]的关键字进行比较,找到位置后将V[i]插入,原来位置上的对象向后顺移。
-
第i次插入排序示例
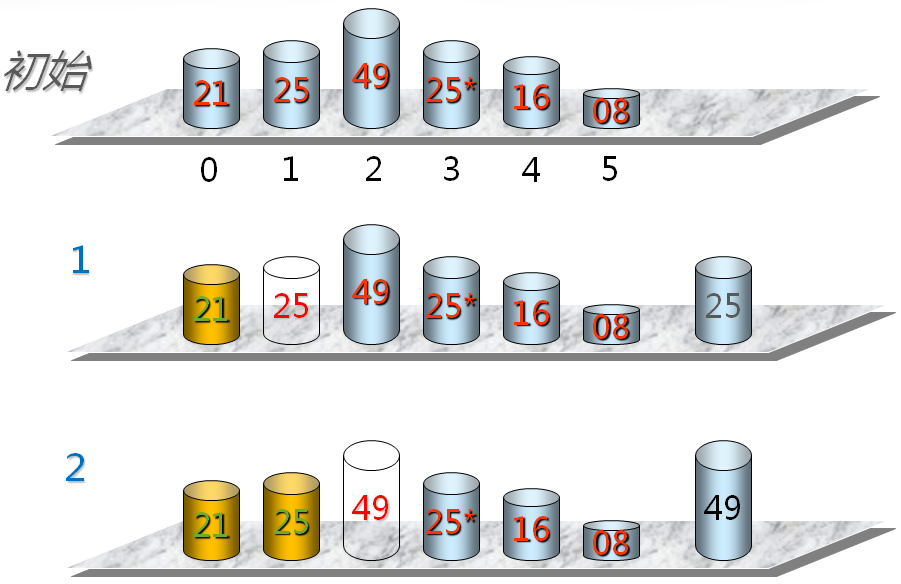
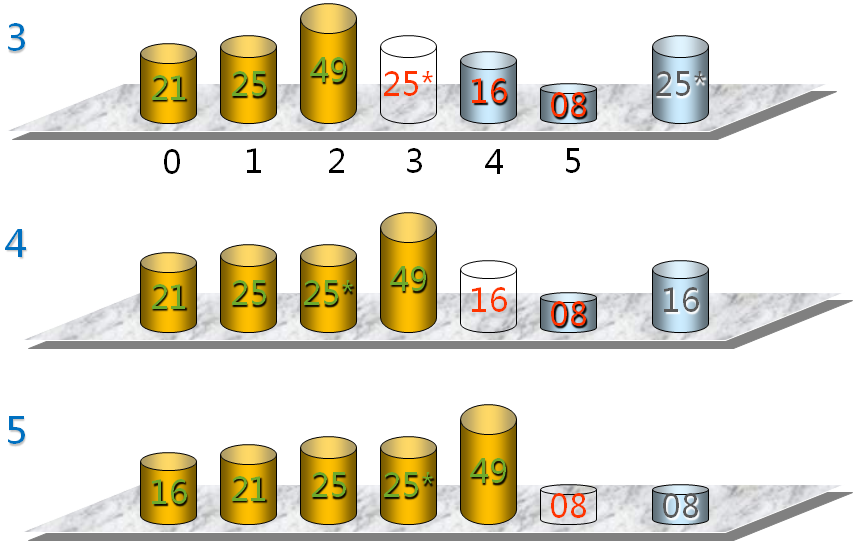
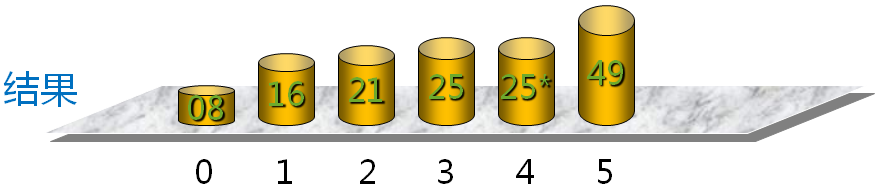
编程实验(二)
-
插入排序的实现
template<typename T>
static void insert(T array[],int size){
for (int i=1;i<size;i++) {
T value = array[i];
int index = i;
for (int j = i-1;j>=0;j--) {
if(value<array[j]){
array[j+1]=array[j];
index = j;
} else
break;
}
if(index!=i)array[index]=value;
}
}
小结
- 选择排序每次选择未排元素中最小的元素
- 插入排序每次将第i个元素插入前面i-1个已排元素中
- 选择排序是不稳定的排序算法,插入排序是稳定的排序方法
- 选择排序和插入排序的时间复杂度为O(n2)